Comparing Proper Fractions (Large Group)

10-B-L-2

Purpose: Refine knowledge of the relative size of proper fractions by comparing

Description: Students compare non-unit proper fractions by reasoning about their relative sizes.

Materials

  • Proper Fraction Numeral Cards
Comparing Proper Fractions

What To Say and Do

  • 1

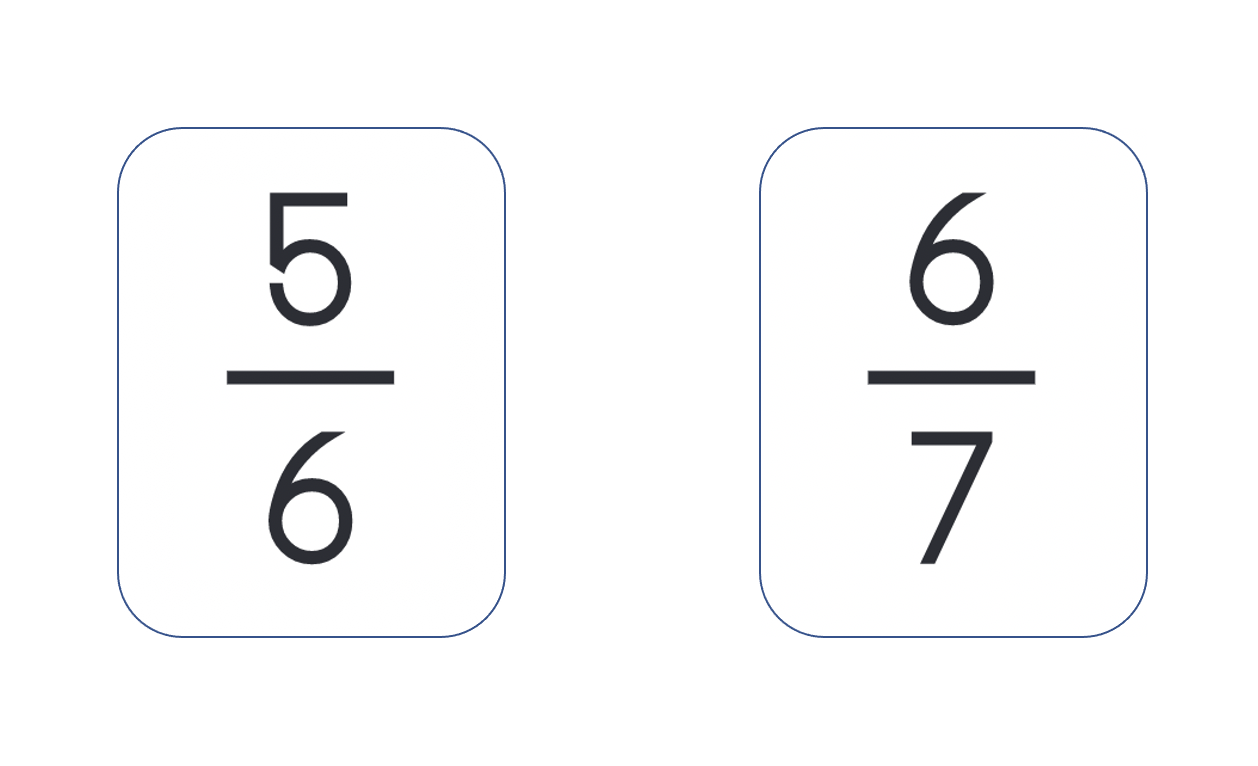
    Select sets of two fraction cards for students to compare. When selecting fraction numerals to be compared, consider the following:

    • Fractions with the same denominator promote reasoning with the same unit of measure (e.g., 5/9 and 4/9) 
    • Fractions with the same numerator but different denominator promote reasoning about the different-sized pieces (e.g., 3/7 and 3/8) 
    • Fractions that are one iteration from whole promote reasoning using knowledge of unit fractions (e.g., 6/7 and 8/9) 
    • Fractions that are just under or over halfway promote reasoning using what students know about halfway (e.g., 3/8 and 4/7) 
  • 2

    Distribute the sets of fraction cards.

  • 3

    Ask students to compare and identify which fraction is bigger and be prepared to share their reason why. Allow ample time for students to collaboratively solve the task in their small groups.

  • 4

    Select students to share for the class discussion based on observations made during the independent discussions.

  • 5

    Facilitate a class discussion using questions such as: 

    • How did you compare your proper fractions? 
    • Of the two fractions, which is bigger/smaller? Why? How did you figure it out? 
    • How can you prove your fraction is the bigger/smaller fraction? 
    • What did you learn that can help you when comparing with other fractions? 
  • 6

    Continue the lesson by distributing new sets of fraction cards for students to compare.

© 2022 US Math Recovery Council®. All rights reserved. Permission is hereby granted for individual use only to support student learning. No other part of this product may be reproduced, stored in a retrieval system, or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, or otherwise without the written permission of the US Math Recovery Council®.